Last night the New York Knicks made a franchise-changing trade when they essentially swapped several players for Carmelo Anthony, a star who has long stated his desire to play in New York. It was a polarizing trade that many have strong opinions about.

Nate Silver of 538 fame made a simple analysis arguing why he believes the trade did not help the Knicks as much as some believe. The central axiom to Silvers discussion is that the goal of an NBA general manager is to:

1. Acquire players who produce above-average value relative to the salaries they are making.

2. Exploit the loopholes in the salary cap so that you spend more money than other teams.

To illustrate his first axiom, Silver used an algorithm developed created by John Hollinger to determine how many wins each player adds to a team. Silver described those players who add many games with a small salary as high in value. Silver argued that, using his metric, Anthony skill to value ratio isnt as high as that of other superstars around the league, and his large salary will end up hindering the Knicks future moves and progress.

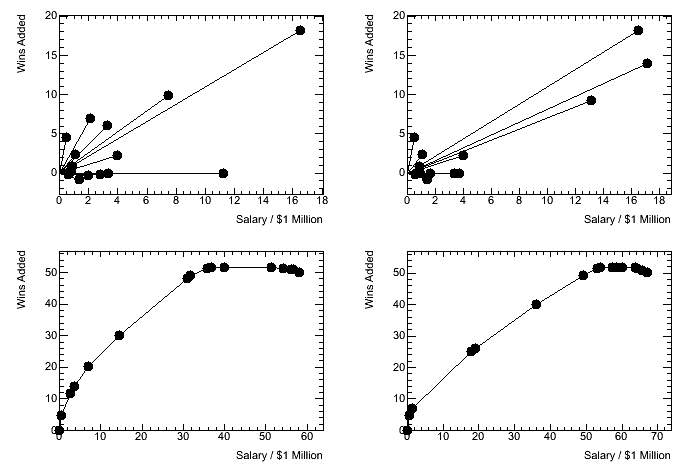
To build upon Silvers arguments, one can see the distribution of the Knicks players in the Salary-Wins plane both before and after the trade:

Distribution before the trade Distribution after the trade

If one were to strictly interpret Silvers method, one would see that the vast majority of wins come from a few players, all of which have a pretty similar ratio of wins to salary. The rest of the players add relatively few wins at the cost of a small amount of salary. Before the trade, the Knicks had several players in a middle range in terms of both wins added and salary cost. Post trade, the Knicks are a much more polarized team, with few high-win players and the rest clustered close to zero in terms of salary and wins.

Yet, simply by looking at these plots, it becomes pretty clear that Silvers model is vastly oversimplified. It treats the majority of players on a team as small line segments only incrementally advancing the teams wins. The reason for this models failure is that it completely factorizes the players on the team: it treats a team as a blind sum of individuals instead of as a collect effort. But anyone who knows basketball, or any sport, knows that this is far from true. Players either enhance or hinder one another. A team consisting of only Carmelo Anthony and four middle-schoolers would not win 14 games against an NBA team because Anthony requires a supporting cast to succeed. And the effects of this cast isnt easily quantifiable in terms of numbers, wins, or salaries.

In sports, there has emerged a false-dichotomy between statistics people and those who understand a game using their instincts. But too often, using statistics in sports means using massive simplifications and trivial models. It means giving too much weight to those things that are easily measurable. And it too often means treating a team as a sum of individuals. While I dont mean to discredit the efforts of the many who have gone a long way to adding legitimacy to sports statistics, I believe the usefulness of those derived numbers models is limited. One should not take them as law. Sports statisticians should do they best they can with the tools and data available, but having created a model or statistic, they should be aware and open to its limitations.